今,2次関数 y=ax 2 bxc があるとき,そのグラフの頂点の座標を (p,q) とすると, a>0 のとき,x=p で最小値 q をとり,最大値はない a(2)2次関数のグラフ ・二次関数y=ax2bxc を y=a(xp)2q の形に変形し、二次関数のグラフをかくことがで きる。(ⅠⅡ部) (観点)知識・理解 (方法)課題・テスト (3)2次関数の決定 ・与えられた条件から,2次関数の式を求めることができる。Y=ax 2 bxc へ拡張し,今後,この形のグラフや性質について調べていくことにしましょう。そこで,次のような目的に基づいてお話をすることにします。 この単元の目的 ① 関数 y=ax 2 bxc のグラフが書けるようになる。 ② 関数 y=ax 2 bxc の性質について
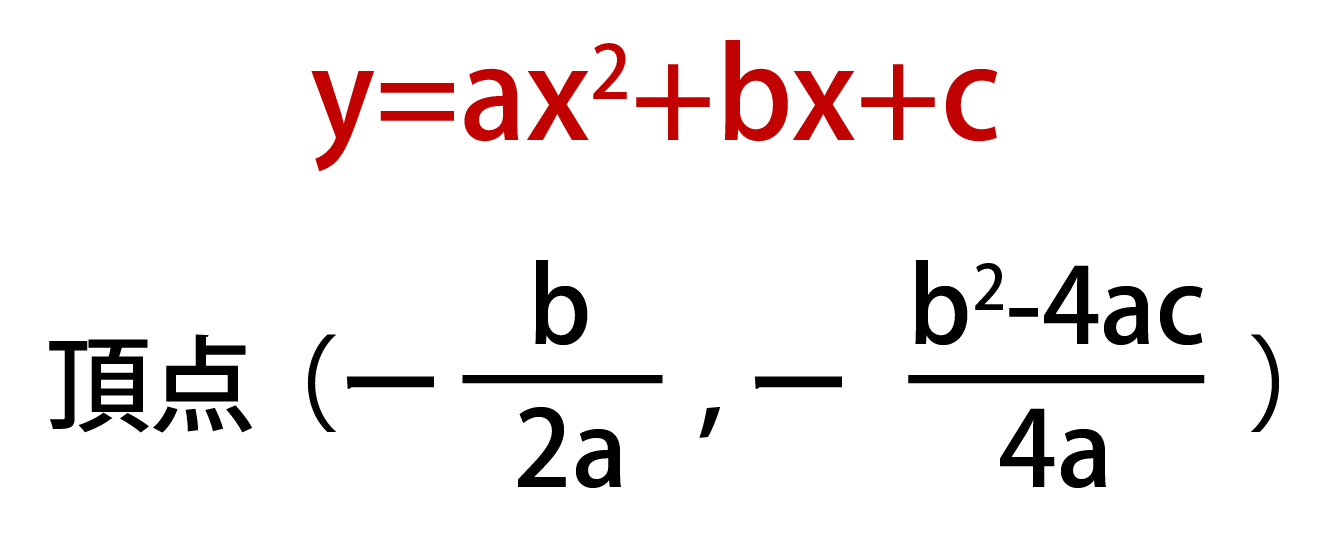
二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ
Y=ax2+bx+c グラフ
Y=ax2+bx+c グラフ-Y=ax 2 bxcのグラフ 動画講義 y=a(xp) 2 qのグラフ 放物線の平行移動(1) このページの学習内容でわからないところがある方例 2次式 y=ax2bxcのグラフ スピンボタンを利用して係数 a, b, c の値を変化させ、2次式 y=ax2bxcのグラフを描いた例を示します。 ※ 頂点の座標を求める際に、a が 0 の場合は除算エラーが発生します。



2次関数とグラフ 勉強動画ラボ 高校数学を中心とした無料の学習動画まとめ
2次関数とは、y=2x23x1のように y が x の2次式で表される関数である。 に、a, b, c を定数(ただし、a≠0)として、次のように表されます。 y=ax2bxc 中学校では、b=0,c=0 の場合だけ扱い、関数y=ax2のグラフが放物線という曲Ax2+bx+cをa(x-p)2+qの形に変形できる。〔技〕 一般の2次関数y=ax2+bx+cのグラフについて,軸,頂点の式 を考察しようとする。〔関〕 グラフの平行移動や対称移動について理解している。〔知〕 与えられた条件から2次関数を求めることができるように x,yの配列データがあって、そのグラフもしくは近似曲線のa,bがもとめたいのでしょうか? 単に値を知りたいだけならば、 1.x、yのデータから散布図でグラフを描く。 2.グラフの曲線部を右クリックし、「近似曲線の追加」を選ぶ。
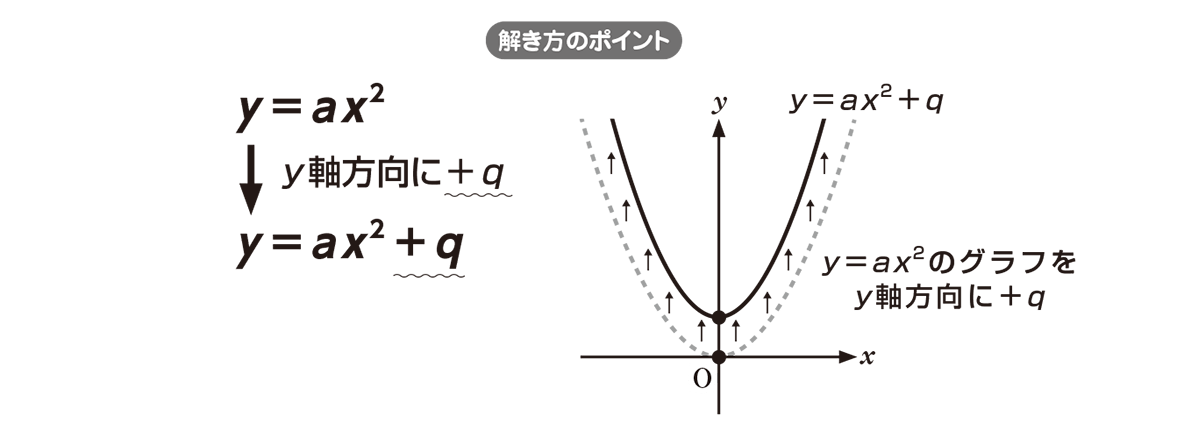
《 高校数学連絡板 》 間違い等のご指摘はこの欄を利用してください. 1.あなたの都道府県名: あなたのペンネームまたはニックネーム: 2.通信欄: どの問題がよかったか・悪かったか,どういう問題を作ってほしいか,間違いの指摘など.二次関数 y=ax2bxc のグラフの特徴について理解し、与えられた条件から、 二次関数の式を求めることができる。 ・定期考査の得点 ・授業態度 ・ 課題等の提出状況 ・基本事項を活 用,応用できるか などを総合的に考える。 3 2章 2次関数 2次関数のグラフ y=ax^2bxc 2次関数のグラフ y =ax2bxc y = a x 2 b x c 2次関数 y =ax2bx2c y = a x 2 b x 2 c のグラフは以下の手順で描く. y =a(x−p)2q y = a (x − p) 2 q の形に式を変形( 平方完成 )する.
これは y = ax2 bx c y = a x 2 b x c の形になっていますね。 このことから何がわかるかというと、 この計算を逆に行えば y = ax2 bx c y = a x 2 b x c は y = a(x− p)2 q y = a (x − p) 2 q の形に変形できる 、ということです。Ax2+bx+cをa(x-p)2+qの形に変形できる。 〔技〕 一般の2次関数y=ax2+bx+cのグラフについて, 軸,頂点の式を考察しようとする。〔関〕 グラフの平行移動や対称移動について理解してい る。〔知〕 根号を含む計算ができるようになる。 2重根号の扱い方1時間 y=ax2bxcのグラフと平方完成 〔コンピュータを活用するねらい〕 (1) pを変化させたときの,y=a(xp)2のグラフの位置の変化を調べる。 (2) pを変化させたときのy=a(xp)2のグラフから,y=ax2のグラフとの関係を見つける。




If Graph Of Y Ax 2 Bx C Is As Shown Then Which Of The Followi




Graphing Y Ax2 Bx C Youtube
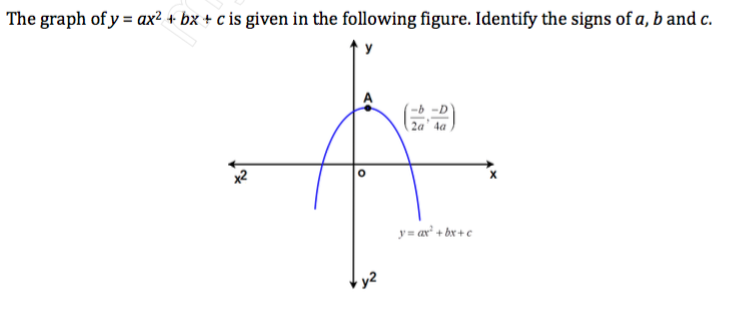
2 次関数y = ax2 bx c のグラフ ら, a > 0のように答えること。また, その理由も書く こと。 (1) a (2) c (3) b 2a (4) b (5) b2 4ac (6) a bc 1 つまり,y=ax 2 bxc という関数を扱うことになります。 これを2次関数と呼んでいます。 2次関数のグラフは,物体を放り投げたときにできる 放物線 と呼ばれる曲線になり,それは頂点を持っています。2次関数 のグラフが右図のように与えられているとき,係数 などの符号を,次のように求めることができます. の符号 の値は「グラフの形」によって決まり,特に の符号は,グラフが下に凸(谷形)のとき ,グラフが上に凸(山形)のとき になります



条件より2次関数の方程式を求める




Y Ax 2 Bx C のグラフのかき方 事前テスト解答例 Kyokuryo Math
2次関数 y=ax 2 bxc の各係数の意味 1次関数y=axbのaは傾きをbはy切片を表していたが、 2次関数の各係数は、グラフのどのような特徴を表しているのだろうか? 係数 a の意味 係数 b の意味 係数 c 二次関数 y=ax^2bxc のグラフの頂点の求め方 二次関数 y = ax2 bx c y = a x 2 b x c のグラフをかくためには、まず頂点を求める必要がありました。 つまり、 y = a(x−p)2 q y = a (x − p) 2 q の形に式変形をする必要がある、ということです。 数学・算数 画像は y = ax2 bx c のグラフである。abcの符号で正しい組み合わせはどれか (1)a>0 (2)a>0 (3)a>0 (4)a<0 (5)a<0 b>0 b<




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ




If A 0 And B 2 4ac 0 Then The Graph Of Y Ax 2 Bx C
2 次関数y = ax2 bx c のグラフ ら, a > 0のように答えること。また, その理由も書く こと。 (1) a (2) b (3) c (4) b2 4ac (5) abc 1 12次関数y=ax²bxcのグラフが下の図のようになるとき、次の値の符号を求めよ (1)a (2)c (3)b/2a (4)b (5)b²4ac (6)abc 22次不等式2x²axb>0の解が1 2次関数のグラフ y=ax2のグラフ 軸はy軸 頂点は原点 a>0のとき下に凸、 a0 a




Y Ax Bのグラフと 切片と傾きの意味 中学数学 By じょばんに マナペディア




54 The Graph Of Y Ax2 Bx C Is Shown In The Given Figu Scholr
平方完成を利用して,2次関数y=ax2+bx+cのグ ラフの軸と頂点を調べ,グラフをかくことができる。 一般の2次関数y=ax2+bx+cのグラフについて, 頂点,軸の式を考察しようとする。 グラフの平行移動や対称移動について理解してい る。ここでは、"y=ax²bxc"のグラフの頂点の求め方についてみていきましょう。 グラフの頂点は、"y=ax²bxc"を 平方完成 して"y=a (x−p)²+q"の形にすることで求めることができましたね。2つのグラフの同じxの値に対するy座標の差を変化させないような変換ととらえます。 (2) より図の斜線部分は長方形OABCの1/3 y=ax2bxcとする。接点PQのx座標をα、βとするときに、それぞれの



放物線と二次関数と根の解の式のグラフ の写真素材 今すぐ編集




高校数学 数 勉強動画 2次関数 の問題 19ch
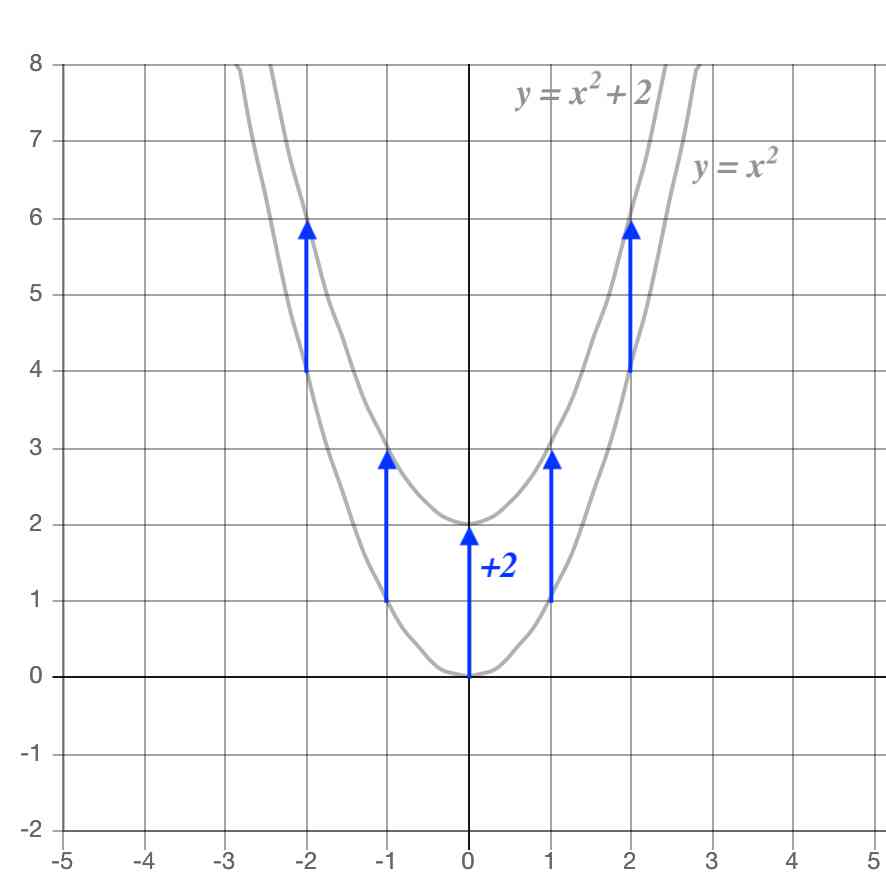
グラフの向きを調べる(上に凸か,下に凸か) y 軸との交点のy 座標(y 切片)の位置を調べる(x 軸より上か,下か) 方法①頂点のx 座標の位置を調べる(正か,負か) 方法②y bx c (y 切片での接線)の傾きを調べる(右上がり(増加)か,右下がり(減少)か) グラフとx 軸の関係(頂点のy 座標)を・y=ax2q のグラフ ↓→例題 ↓y=ax2q のグラフy=ax2q のグラフを y=ax2 のグラフと比較しながら考えてみます。やはり表を作ってみることが大切です。 下の表は 2x2 と 2x21 を比較したものです。 xのどの値においても, 2x21 の値は 2x2 の値に1を足したものです。したがって, y=2x21 のグラフは y=2x2Y = ax2b のグラフ 年 組 番 氏名 例1 関数y = x2 3のグラフをかきなさい。 5 10 x y O x = 1のとき, y = 1 2 3 = 4 x = 2のとき, y = 2 2 3




3 の文章の意味が分かりません グラフ等を使って教えてください Clear



Exploring Parabolas Y Ax 2 Bx C
時間 授業内容・活動 留意点 15分 1.y=ax2bxcのグラフ y=ax^2bxcgpsを開き,a,cを変化させて,グラフの変化を確認する。(教Grapes・生徒) bを変化させたとき,グラフがどのように変化するかを観察して考察する。のグラフは、y=ax2 のグラフをx軸方向にp、y軸方向にqだけ平行移動した放物線である。 軸は直線x=p、頂点は点(p,q)、a>0の時は下に凸、a<0の時は上に凸で描かれる。 また、2次関数y=ax2+bx+cは、変形すると、 §17 関数とグラフの意味 §18 2次関数 y=axpg2qのグラフ §19 2次関数 y=ax2bxcのグラフ § 2次関数の最大値・最小値 §21 2次関数の決定 §22 2次方程式の復習 §23 2次方程式の判別式 §24 2次関数のグラフと座標軸の共有点




The Given Figure Shows The Graph Of The Polynomial F X Ax 2 Bx C Then Ltbr Gt 1 Nbsp Youtube




高校数学 Y Ax 2 Bx Cのグラフ 映像授業のtry It トライイット
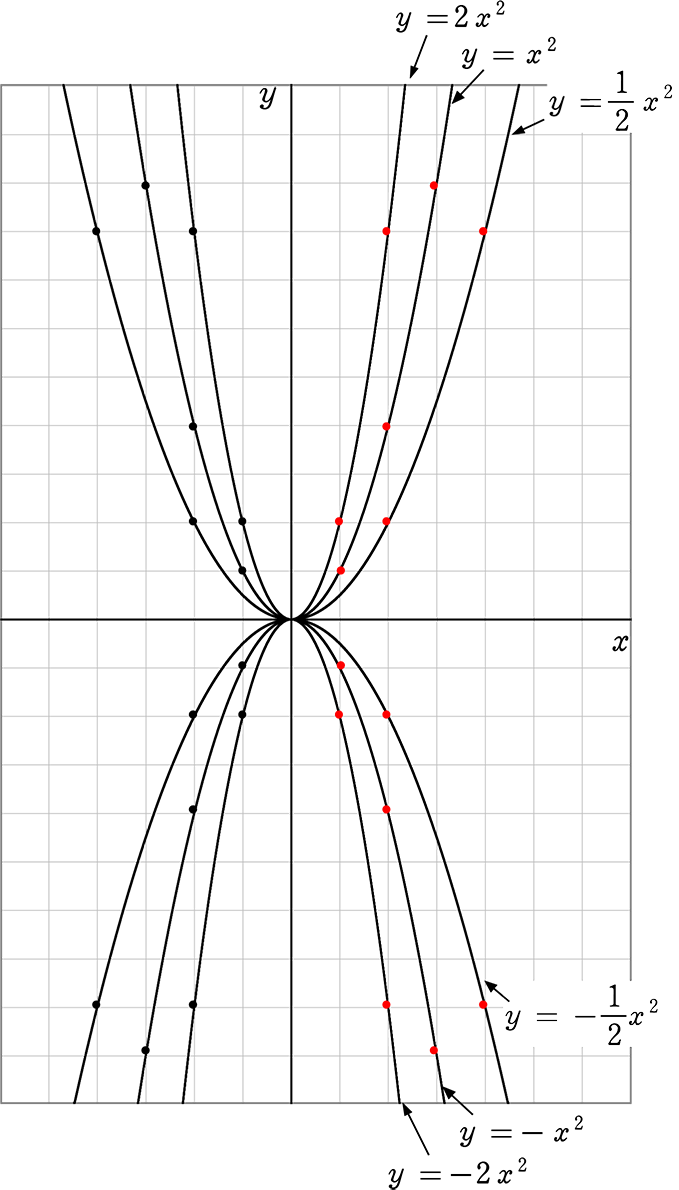
2次関数 y = ax2 + bx + c のグラフと x 軸の共有点の座標は,( x ,0)とおける,すなわち, y =0であることを理解しておきましょう。二次関数の一般式は y=ax^2bxc です 例 2次式 y=ax2bxcのグラフ スピンボタンを利用して係数 a, b, c の値を変化させ、2次式 y=ax2bxcのグラフを描いた例を示します。 ※ 頂点の座標を求める際に、a が 0 の場合は除算エラーが発生します。この例では、ISERROR<グラフの称> <関数y=ax2 のグラフの特徴> <グラフの開き> ・線対称、線対称、x軸の上側にあるということ を記載 y=2x2 のグラフとy=x2 のグラフを比べる →y=1 2 x2 のグラフ →y=ax2 で、a




Find The Sign Of A B C In Ax 2 Bx C Given The Graph And A Coordinate On It Mathematics Stack Exchange



2次関数とグラフ 勉強動画ラボ 高校数学を中心とした無料の学習動画まとめ
中学3年の問題をイチから解説! |中学数学・理科の学習まとめサイト! y=ax2乗の利用放物線と直線による面積! 中学3年の問題をイチから解説! 放物線と直線そして、面積 マジで難しそうなんだけど というわけで、今回は中3で学習する中にはグラフが折れ線になってしまうものがいる。放物線という曲線をもっと身近に体験 させる方法を工夫する。 (3)y=ax2bxcの グラフは,y=ax2の グラフを平行移動して得られるが,そ の際y・=aX2bxcの 右辺を変形(平 方完成)す る必要が生じる。その結果,平 方Ax2+bx+cをa(x-p)2+qの形に変形する。〔技〕 1次関数のグラフを描き,値域を求める。〔知〕 第2回定期考査① 放物線y=ax2の形や軸,頂点について理解する。〔知〕 ワーク 第3章 数学Ⅰ 第1節 2次関数とグラフ



2次関数のグラフと係数




21 Y X4 Y Ax2 2 A B Descubre Como Resolverlo En Qanda
215 連立1次方程式の解とグラフ 22 因数分解と平方根 221 因数分解 222 平方根の利用 23 2次関数のグラフ 231 y=ax2のグラフとy=ax2qのグラフ 232 y=a(xp)2のグラフとy=a(xp)2qのグラフ 233 y=ax2bxcのグラフ 234 Excelで描くグラフの正確さ




Graph Of Y Ax 2 Bx C Is As Shown In The Figure If




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ




22 Yax2bxc A B Cgeq X Descubre Como Resolverlo En Qanda



The Graph Of Y Ax 2 Bx C Is Given In The Chegg Com



Quadratic Graph Example Y Ax C Expii




高校数学を初めから丁寧にvol 044 数学i 二次関数 Y Ax 2 Bx Cのグラフ 平方完成をマスターしよう Youtube



二次不等式とは 解き方や解の範囲の求め方 判別式の問題 受験辞典
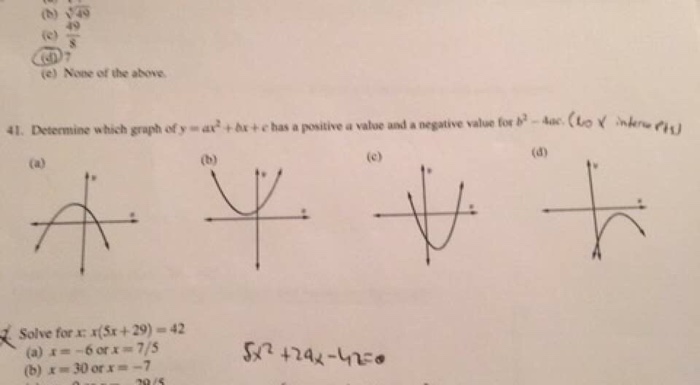



Determine Which Graph Of Y Ax 2 Bx C Has A Chegg Com



中学数学 関数



高校数学 Y Ax 2 Qのグラフ2 映像授業のtry It トライイット



2次関数y Ax Bx Cのグラフが次の図のようになるとき Yahoo 知恵袋




Y Ax 2 Bx Cのグラフ 数学i フリー教材開発コミュニティ Ftext




2次関数のグラフと直線




Consider The Graph Of Quadratic Trinomial Y Ax2 Bx C As Shown In The Figure Where X1 And X2 Are Roots Of The Maths Complex Numbers And Quadratic Equations Meritnation Com




Bとcとa B Cの求め方が分かりません 教えてください Clear




Use The Graph Of Y Ax2 Bx C To Solve A Chegg Com




2次関数のグラフ
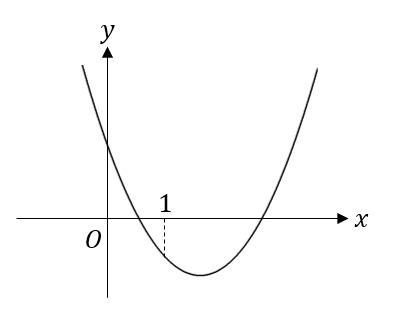



二次関数 係数の符号の決定 グラフから符号を決めるポイントを解説 数スタ




2次関数のグラフと係数



2次関数とは 1分でわかる意味 公式と計算 グラフ 平行移動との関係



2次関数y Ax 2 Bx Cのグラフが図のようになるとき 次の値の符号を求 Yahoo 知恵袋




Y Ax2 Bx C Graph Novocom Top



Y Ax 2




中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく



文字係数2次関数の頂点



2次関数とは 1分でわかる意味 公式と計算 グラフ 平行移動との関係




If The Diagram In Fig 2 22 Shows The Graph Of The Polynomial F X Ax Bx C Then A A Gt 0 Brainly In
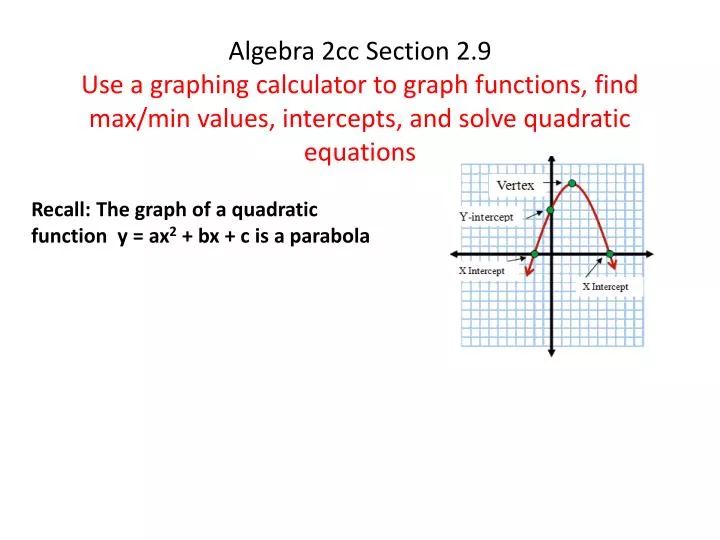



Ppt Recall The Graph Of A Quadratic Function Y Ax 2 Bx C Is A Parabola Powerpoint Presentation Id




中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




二次関数 グラフと係数の符号 二次関数y Ax 2 Bx Cのグラフで Okwave



21 Y X4 Y Ax2 2 A B Descubre Como Resolverlo En Qanda
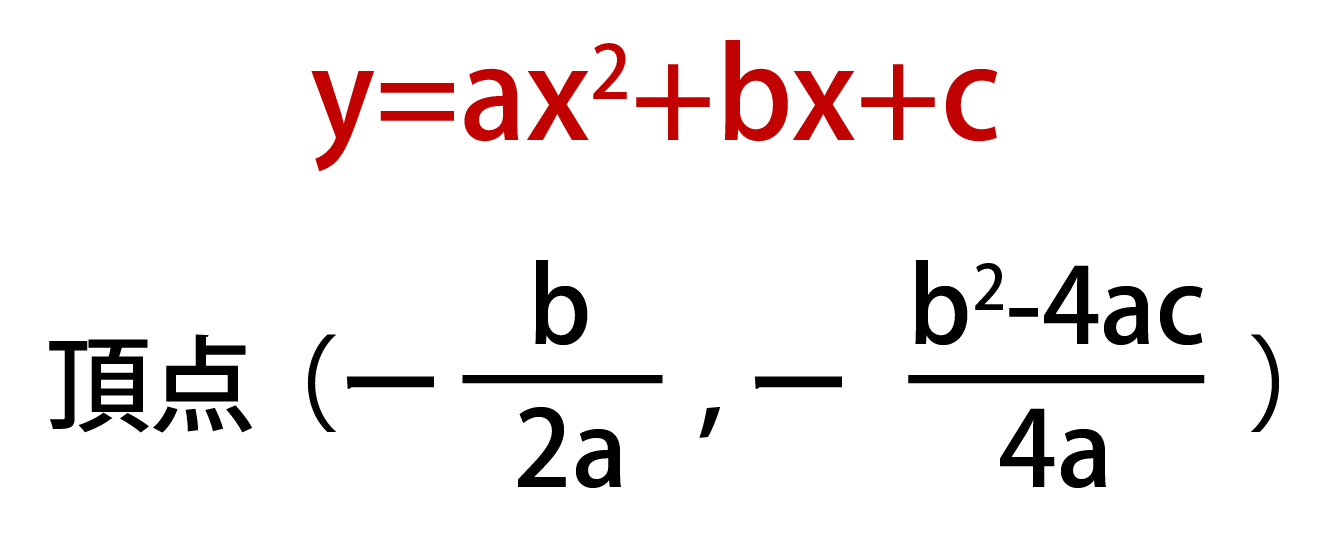



二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ
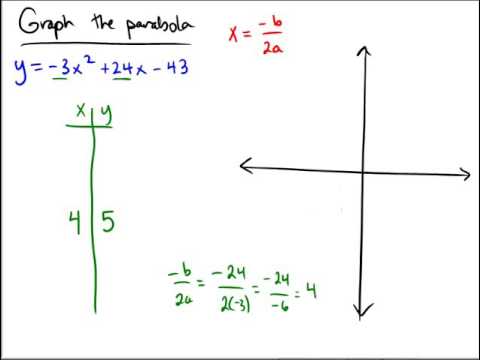



Graphing A Parabola Of The Form Y Ax 2 Bx C Integer Coefficients Youtube




二次関数のグラフは全て相似 数学 二次関数 そーまのブログ屋さん




高校数学 Y Ax 2のグラフ 下に凸 上に凸 映像授業のtry It トライイット




高校数学 Y Ax 2 Bx Cのグラフ 練習編 映像授業のtry It トライイット
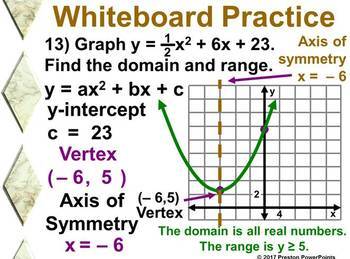



Alg 1 Graphing Y Ax2 Bx C In A Powerpoint Presentation Tpt




高校数学 Y Ax 2 Bx Cのグラフ 例題編 映像授業のtry It トライイット



Y Ax 2



二次関数のグラフの書き方




Y Ax 2 Cのグラフ 数学i フリー教材開発コミュニティ Ftext



Search Q E6 8c 87 E6 95 B0 E9 96 E6 95 B0 B0 95 Tbm Isch




高校数学 Y Ax 2 Bx Cのグラフ 例題編 映像授業のtry It トライイット



The Graph Of The Polynomial Y Ax2 Bx C Is Shown In Fig 2 2 Write The Value Of B2 4ac Y Ax2 Bx C From Mathematics Polynomials Class 10 Haryana Board English Medium




The Graph Of The Function F X Ax 2 Bx C Presented In One Problem Download Scientific Diagram



Y Ax2 Bx Cのグラフで 上に凸だったらaの値はマイナスだとわか Yahoo 知恵袋



1



Quadratic Graph Example Y Ax C Expii



二次関数のグラフの書き方




Graph Of Ax2 Bx C Novocom Top



1
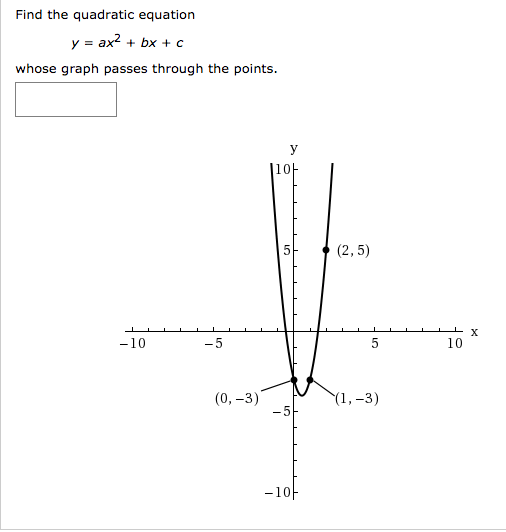



Solved Find The Quadratic Equation Y Ax2 Bx C Whose Chegg Com




基本 二次関数 Y Ax 2 のグラフ なかけんの数学ノート
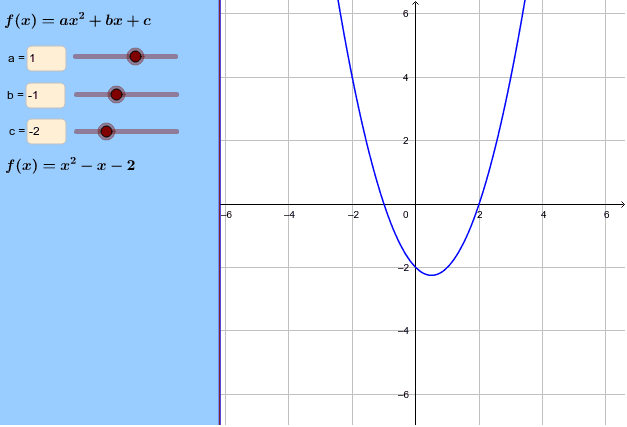



The Graph Of Y Ax 2 Bx C Geogebra



Unique Quadratic Equation In The Form Y Ax 2 Bx C
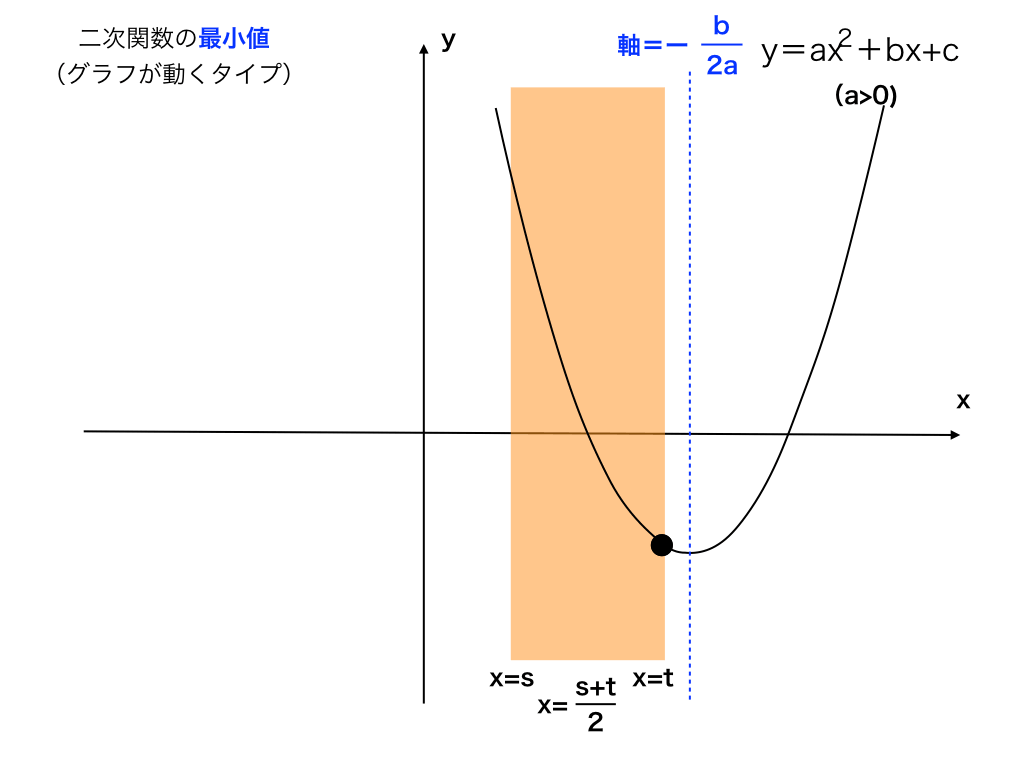



二次関数の最大値 最小値の求め方 グラフや定義域が動くタイプ



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola
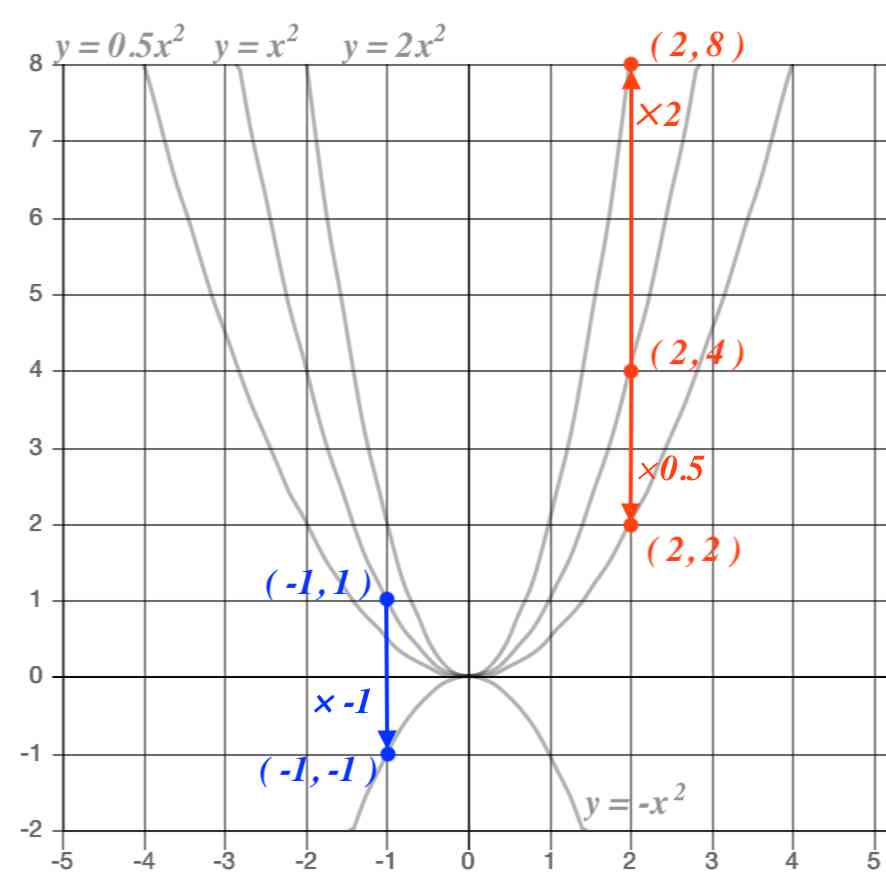



二次関数のグラフの書き方



2次関数y Ax 2 Bx Cのグラフが 次のような図で与えら Yahoo 知恵袋
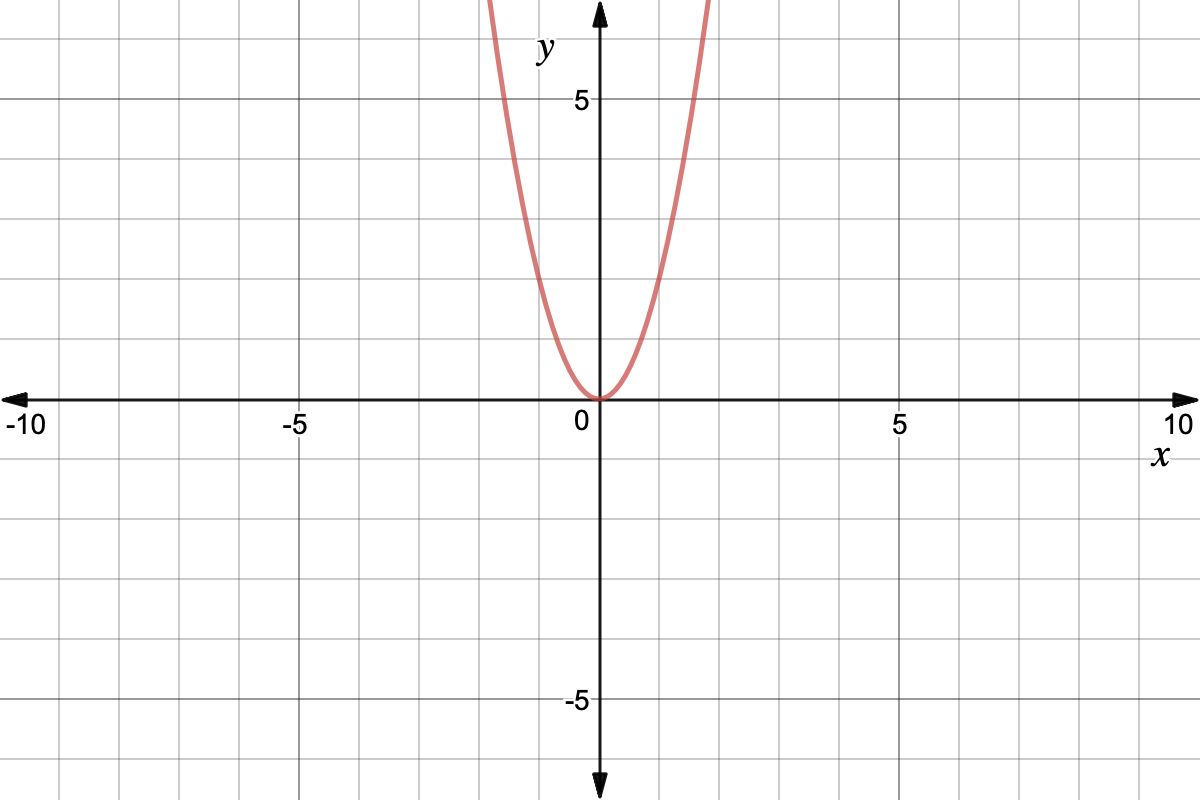



Quadratic Graph Example Y Ax Expii



To Investigate The Effect Of The Constants A B And C On The Graph Y Ax2 Bx C Gcse Maths Marked By Teachers Com




数学教材 中間発表



Y Ax 2 とy Bx Cを足す
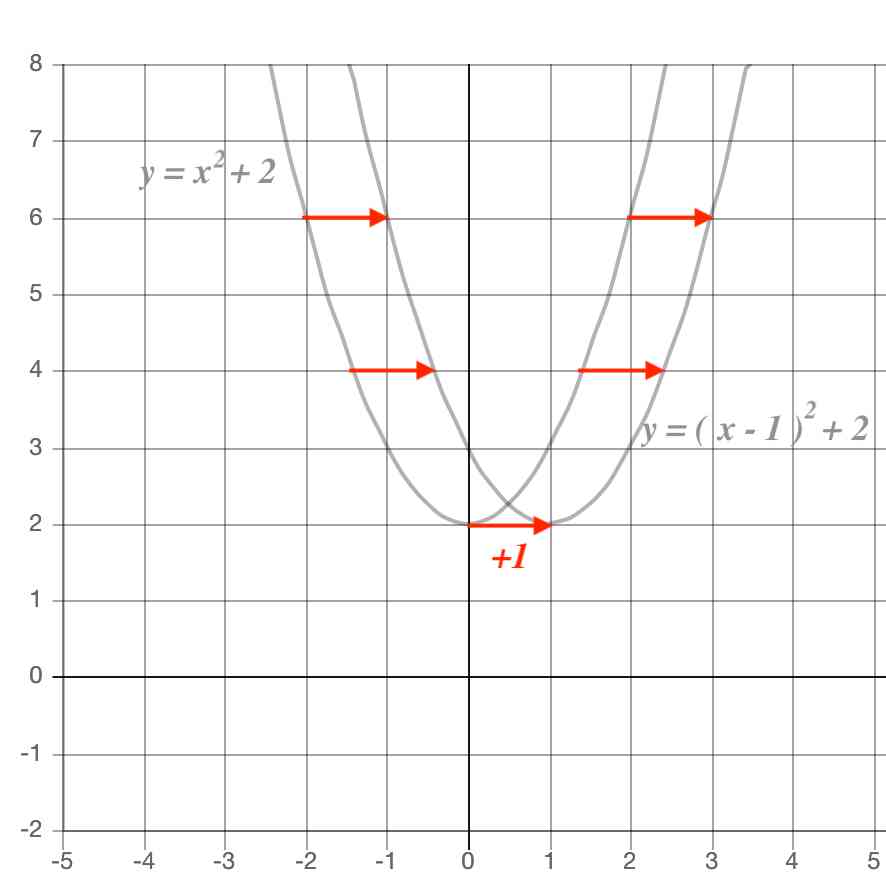



二次関数のグラフの書き方




75 Yax2 最高のぬりえ



To Investigate The Effect Of The Constants A B And C On The Graph Y Ax2 Bx C Gcse Maths Marked By Teachers Com



2次関数 Y Ax 2 Bx Cのグラフについて Y Ax 2 Yahoo 知恵袋




Ax 2 Bx C 0 Graph Novocom Top




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ




Figure 2 23 Show The Graph Of The Polynomial F X Ax2 Bx C For Which Mathematics Shaalaa Com
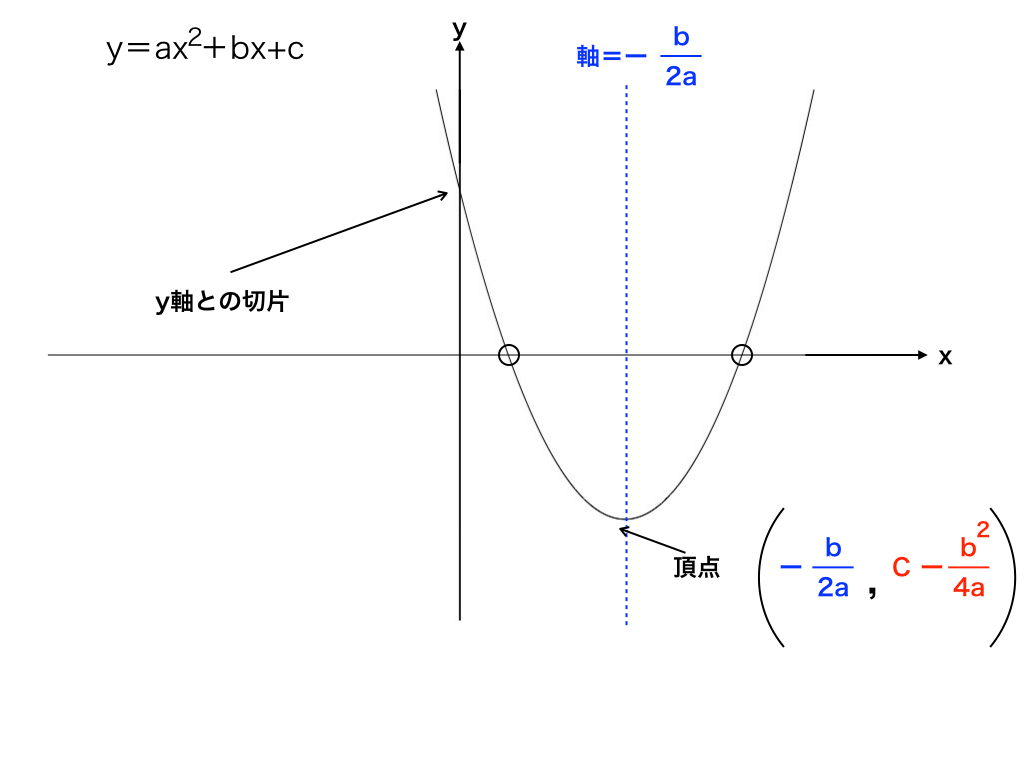



二次関数のグラフと解の存在範囲の問題をわかりやすく解説
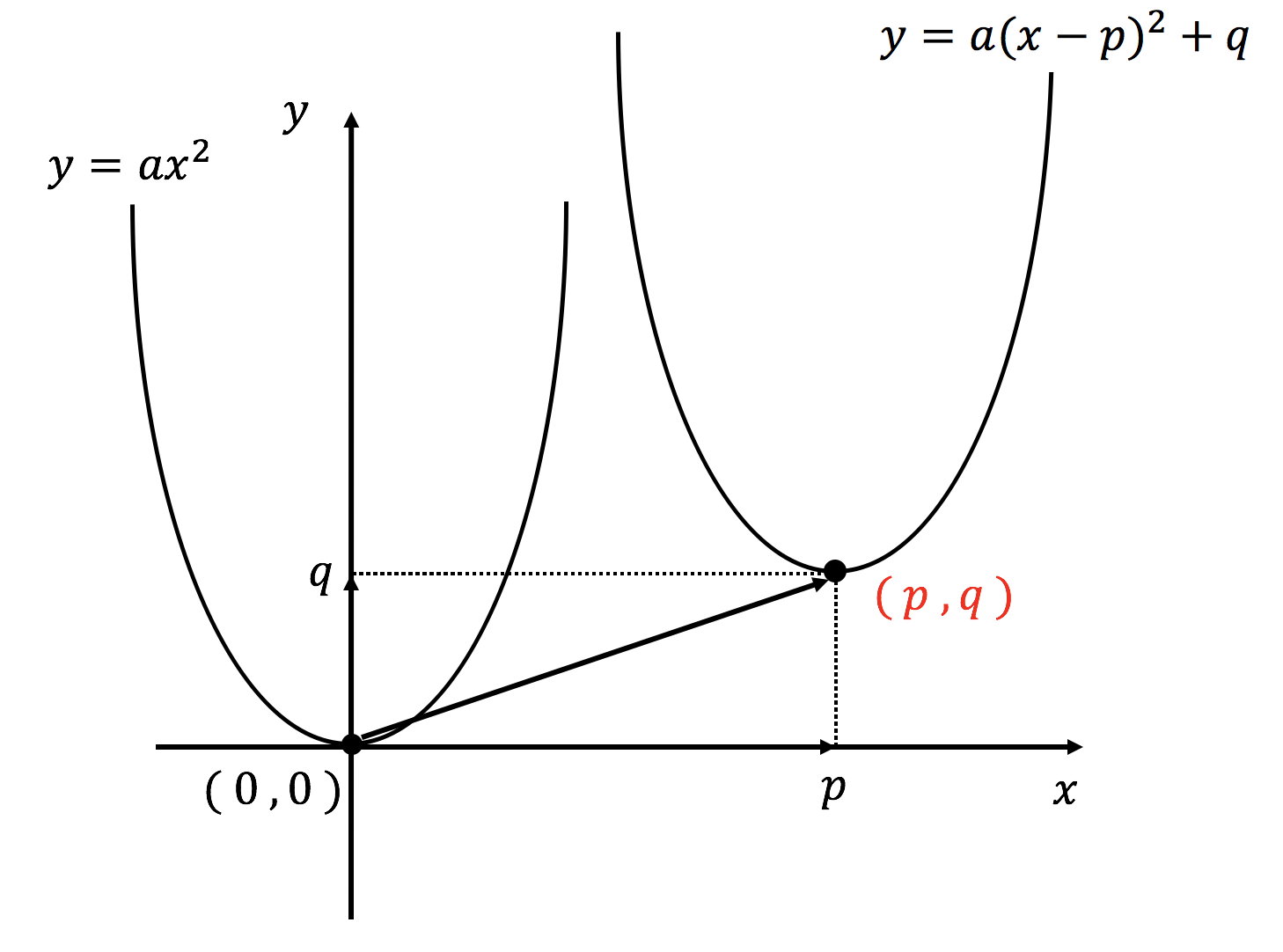



3分で分かる 二次関数の頂点の求め方をわかりやすく 練習問題付き 合格サプリ
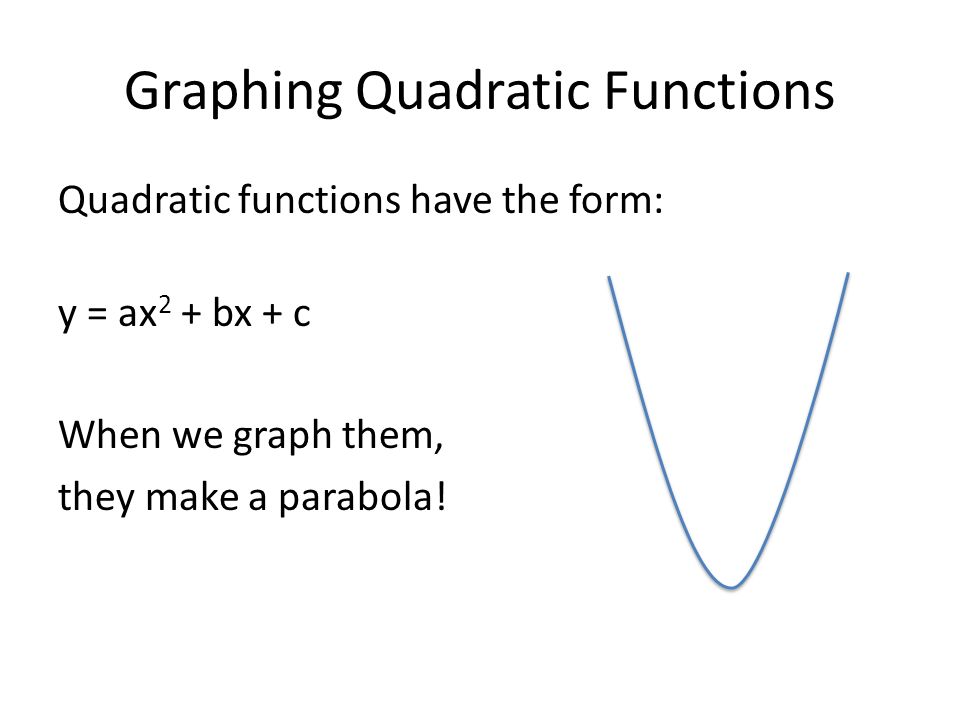



Graphing Quadratic Functions Quadratic Functions Have The Form Y Ax 2 Bx C When We Graph Them They Make A Parabola Ppt Download




Classzone Chapter 4




Y Ax 2 Bx Cのグラフ 数学i フリー教材開発コミュニティ Ftext



The Graph Of Y Ax 2 Bx C Has A Minimum At 5 3 And Passes Through 4 0 How Do I Find The Values Of A B And C Quora




2次関数のグラフと方程式




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ




Y Ax 2 Bx C のグラフのかき方 事後テスト解答例 Kyokuryo Math



1




標準 二次関数y Ax 2 Bx Cのグラフ 具体例 なかけんの数学ノート




Y Ax 2 Bx Cのグラフ 数学i フリー教材開発コミュニティ Ftext




2次関数 Y Ax 2 Bx C のグラフのかき方 大学受験のための数学思考法




高校数学 2次関数のグラフy Ax Bx Cの係数の符号 受験の月



辞書 二次関数のグラフの特徴 わかりmath



0 件のコメント:
コメントを投稿