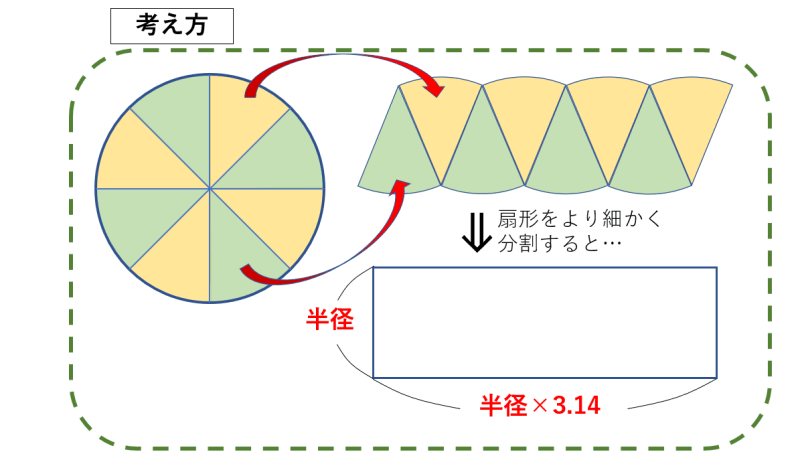
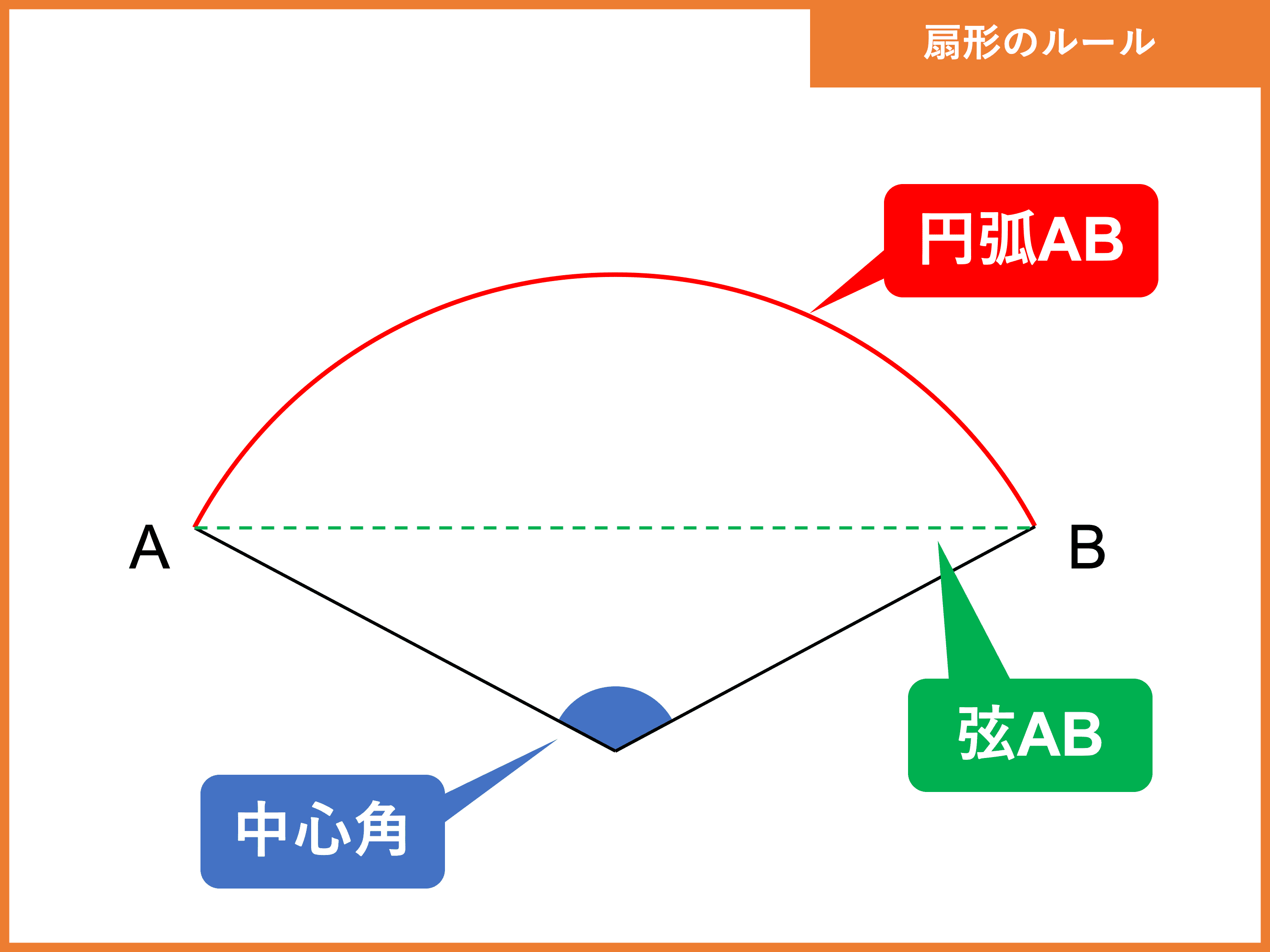
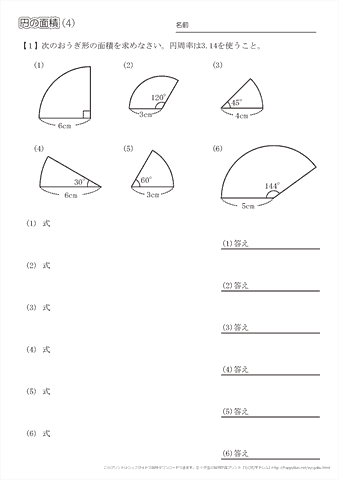
面積は当然、底辺×高さ× で求められるので、以下の通りです。 = = こうした一般的な解き方でも1分以内に解答したいところですが、今回教える2大公式によって高さ2秒、面積3秒、合わせて5秒で答えを出すことができます。 その公式がこちらです。 aよって,楕円の面積公式より答えは π ⋅ 3 ⋅ 4 = 12 π \pi \cdot 3\cdot 4=12\pi π ⋅ 3⋅ 4 = 12π ここから,楕円の面積公式の3通りの証明を紹介します。 グラフの拡大を用いる方法 愚直に定積分を計算する方法 ガウスグリーンの定理を使う方法 1は積分を知らです。 (πは円周率:π=←無限に長い小数になるからギリシャ文字πで表すことになっている) 半円の面積は,円の面積の半分だから 3分の1円の面積は,円の面積の3分の1だから 4分の1円の面積は,円の面積の4分の1だから 一般に中心角の扇形の面積は,円の面積のx/360だから 例題1 半径がa(cm2)で中心角が45°の扇形の面積S(cm2)は 例題2

円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり
扇形の面積の求め方 小学生
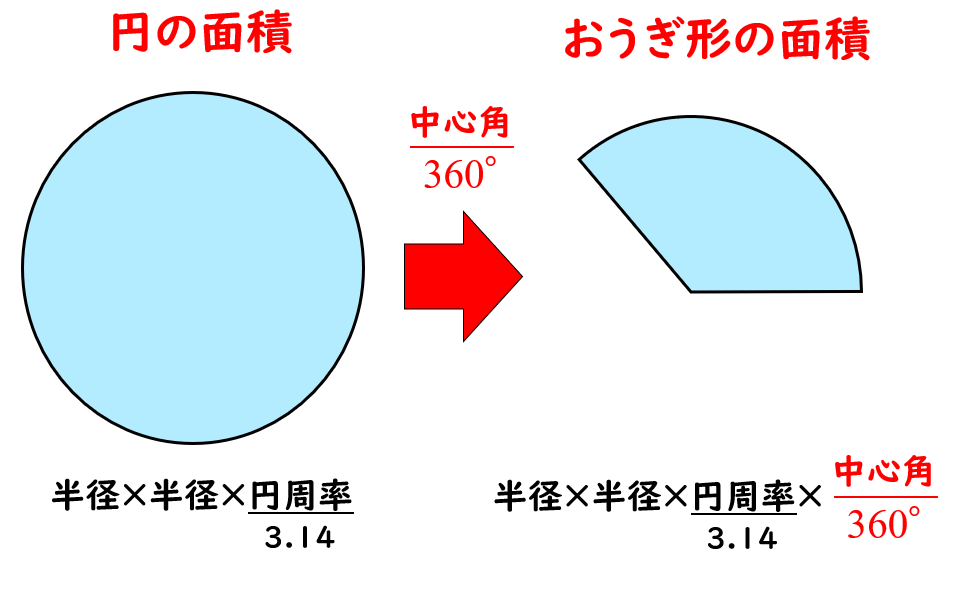
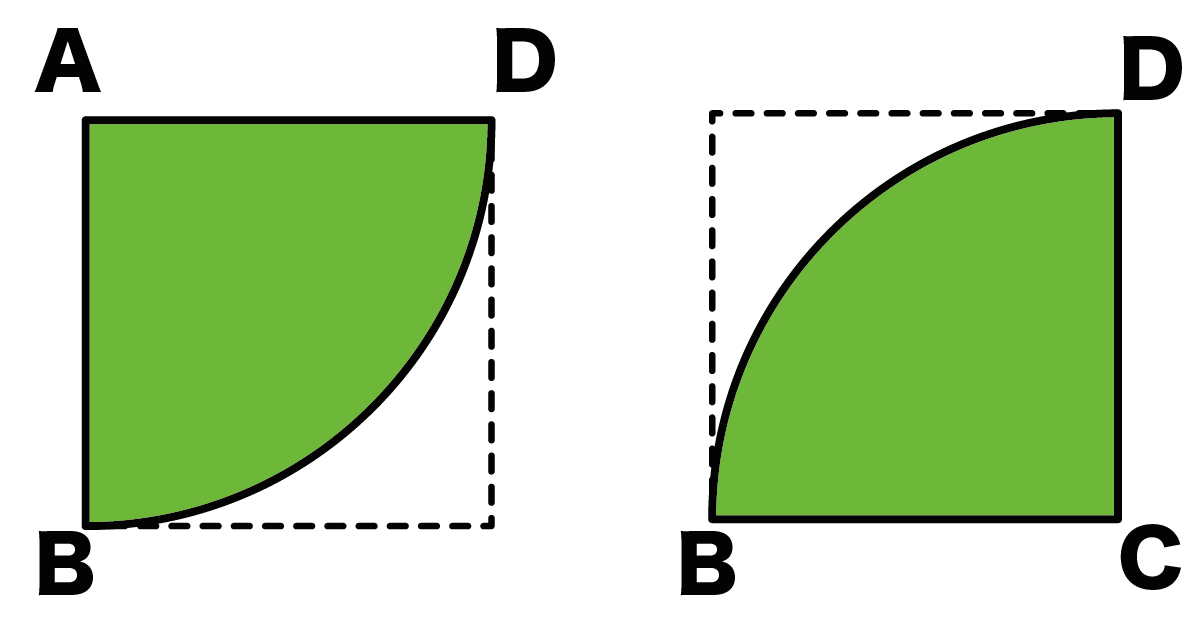
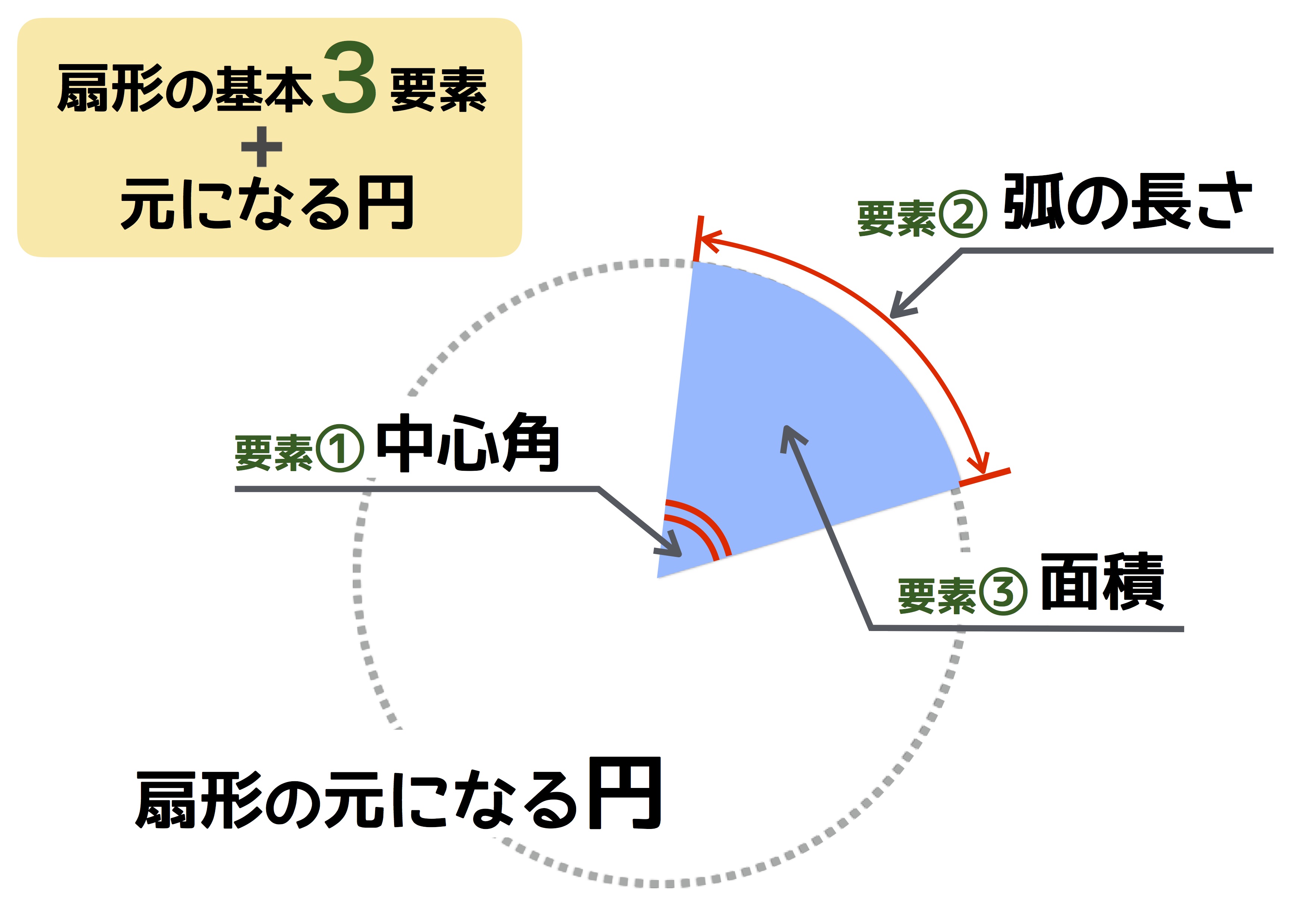
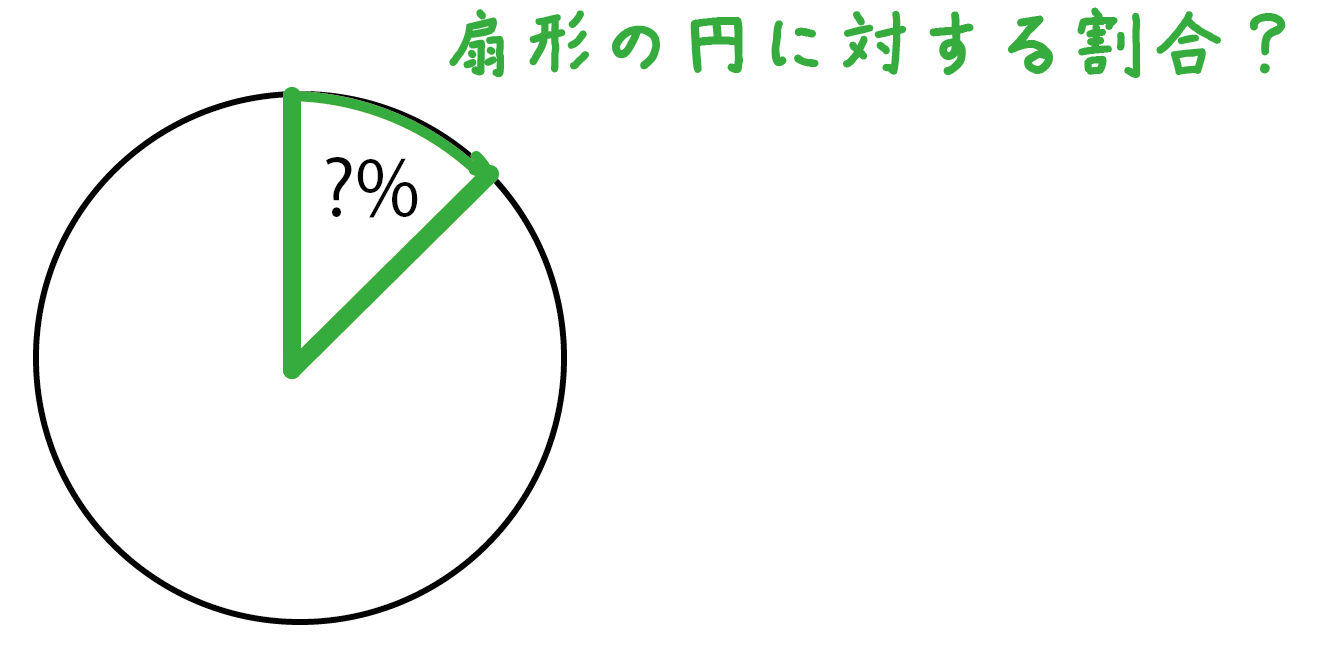
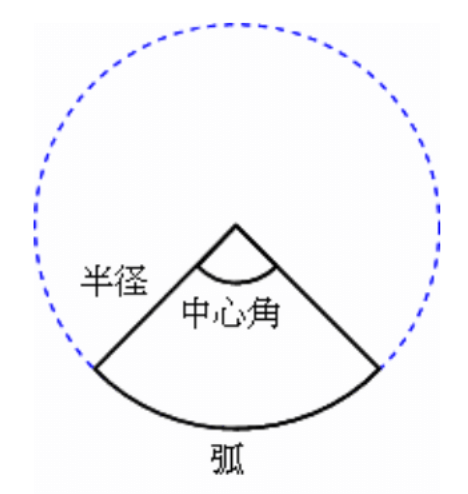
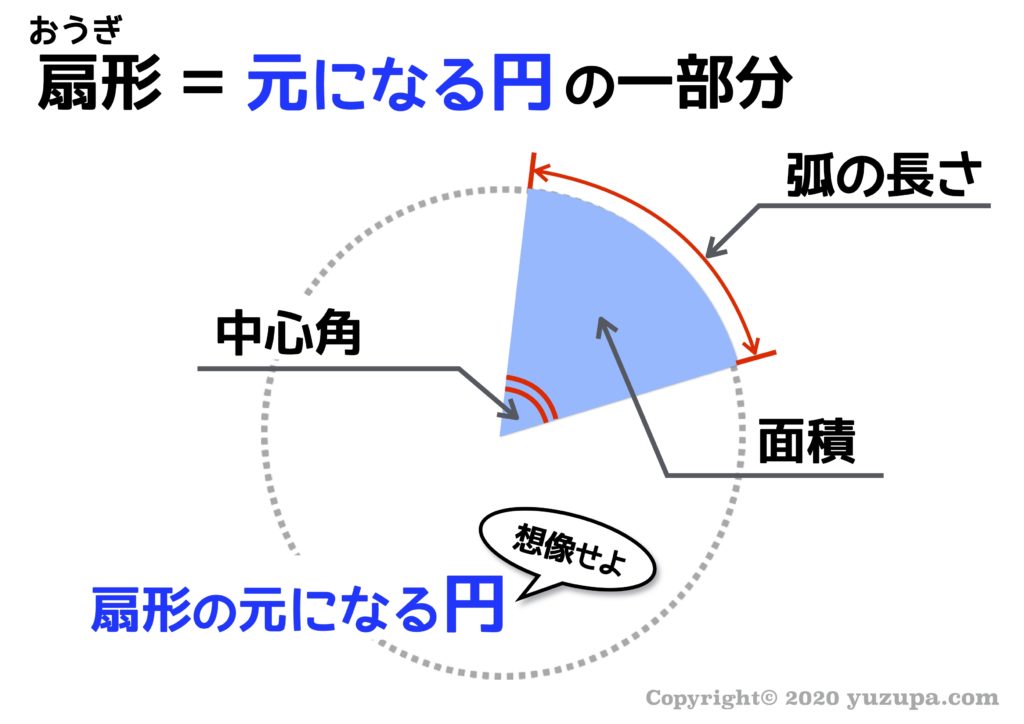
扇形の面積の求め方 小学生-面積の求め方 扇形 扇形の面積を求める公式は、次の通りです。 S = πr2 × x 360 = 1 2lr S = π r 2 × x 360 = 1 2 l r 中心角 x°、半径 r の扇形 ここで、S は扇形の面積、π は円周率、r は円の半径、x は中心角(単位「度」)を表します。 また、2行目の l は扇形の弧の長さを表します。 このページの続きでは、この 公式の導き方 と、 扇形の面積を求める計算問題の解き方おうぎ形の面積 = 円の面積 × 中心角 360° 中 心 角 360 ° = 半径×半径×314 × 中心角 360° 中 心 角 360 ° 重要なのは、 おうぎ形が元の円と比べた時にどれくらいの割合なのか ということ。 たとえば中心角が 270° 270 ° 、 180° 180 ° 、 90° 90 ° 、 45° 45 ° といったおうぎ形は元の円と比べるとそれぞれ 3 4 3 4 、 1 2 1 2 、 1 4 1 4 、 1 8 1 8 の大きさになっているのは明らか




円錐の表面積 中心角を求める問題を丁寧に解説 数スタ
今回は扇形(おうぎ形)の面積・弧の長さ・まわりの長さの求め方について書いていきたいと思います。 扇形(おうぎ形)の面積の求め方 小6 算数「面積」1 組 番 氏名 千葉県図のように、1辺が8cmの正方形がたて、よこ3cmずつずれて重なっています。黒くぬった部分の面積を求めなさい。 → 解答 問題11 図のように、1辺がcmの正方形の中に円が4個あります。黒くぬった部分の面積を求めなさい。円周率は314とします。扇形の面積・弧の長さ・まわりの長さの求め方 ★円錐の表面積★簡単な求め方とその理由を解説 円の面積のおもしろ問題3選!美味しそうな色 扇形の面積は?1分でわかる意味、公式、求め方 おうぎ形の弧の長さと面積の求め方|小学生に教
正方形・長方形の面積の求め方|小学生に教えるための分かりやすい解説 管理人 9月 17, 18 / 11月 26, 18 それだけに、図形の面積の概念を学ぶ重要な単元です。 扇形の面積=半径×半径×円周率× 中 心 角 360 ° ※扇形の面積は、円の面積に 中 心 角 360 ° をかけることで求めることが出来ます。 ※円周率は、小学校ではふつう314を使います。 側面である扇形の面積を求めようとすると、扇形の公式から分かるように 中心角が必要になります。 というわけで、 まずは扇形の中心角を求めていきます。 底面の円周の長さと側面の弧の長さが等しいことを利用すると
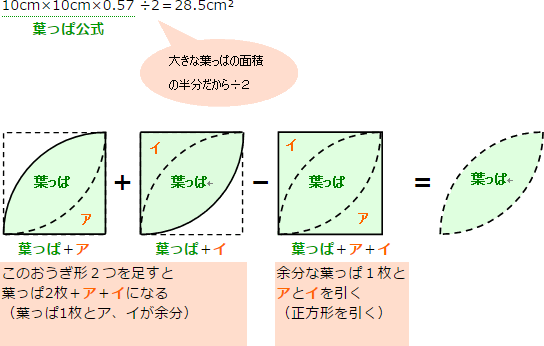
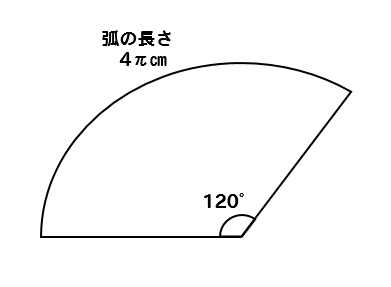
葉っぱ1枚分の面積を求めて4倍すれば、四つ葉の面積になります。 右の図のように、四つ葉を 分解 して考えると、葉っぱ1枚が入っている正方形の一辺の長さは、5cmです。 葉っぱ1枚分の面積は、葉っぱ公式により 5cm×5cm×057=1425cm² よって 四つ葉の面積は まとめ:扇形の面積は「おうぎ形パワー」を円にかける 扇形の面積の求め方はどうだった? ? 円の公式に毛がはえたようなもんだから、頑張れば覚えられそうだね。 S = πr² × α / 360 「円とおうぎ形」がテストにでるときに確認したいね^^ おうぎ形の面積をマスターしたら次は おうぎ形の中心角 を求めてみよう! Qikeru:学びを楽しくわかりやすく 4 Pockets 問題文に面積が与えられているので、円と扇形の面積を比較しながら中心角を求めます。 半径が4㎝の円の面積は、\(\pi\times 4^2=16\pi(cm^2)\) 半径が4㎝の扇形の面積は、問題文より \(4\pi(cm^2)\) です。




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり




円 扇形 の面積 周や弧の長さの公式 数学fun
おうぎ形 面積 求め方 小学生 おうぎ形 面積 求め方 小学生中1 数学 空間図形9 おうぎ形の公式 17分 Youtube おうぎ形の面積の求め方 次世代型個別指導塾アチーブメント Achievement東京都の小学生 じゃじゃじゃ さんからの解答。 π=3とする 扇型の半径を4とする 扇形の中心角を90°とする 扇形の面積は 扇形の弧の長さは 等しくなった 扇形の面積=弧の長さ×半径×1/2 これを「弧の長さ×半径×1/2」に代入すると円の面積 「半径×半径×円周率」で求められる円の面積。 いろいろな大きさの円の面積を計算してみよう。 動画で学ぼう! (NHK for School) 円の面積の求め方を、四角に直すことで原理から考える




扇形の弧の長さの求め方 公式と計算例




タダ塾 小6算 円の面積5 連問2 Youtube
ひし形の面積 平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積 円の面積から半径 扇形の面積面積の公式が,直接使えない形の面積は,どうやって求めるの 13 下のような,くぼんだ形の面積は,どうやって求めればいいの 14 長方形の土地に畑と道を作ったとき,畑だけの面積の求め方を教え小学生でも公式を簡単に使える問題です! 中学や高校の数学の計算問題 扇形の面積の求め方! 小学生でも公式を簡単に使える問題です! 中学や高校の数学の計算問題 学び カテゴリーの変更を依頼 記事元 suugakunomondaihatenablogcom エントリーの編集




面積の求め方 算数の教え上手 学びの場 Com




簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
これらの情報を元に、扇形の表面積を求めて生きたいと思います。 扇形の面積 = 底面の円の面積 + 扇形の面積 = r × r × π + ( l × l × π ) × 2rπ / 2lπ = r 2 π + lrπ これで、扇形の表面積を計算することができました。面積の公式Javaで教材を 面積の公式、数値入力による面積の計算。公式のたしかめや計算の確かめに利用できます。 top情報室へ 半角の数字をお使いください。by sakata 100:面積=1:057 面積=57㎠ と求めることができる。 円周率が314の時しか使えません。 公式として覚えているだけでは、中学生になってから問題を解けなくなってしまいます。 基本的な考え方で求められるようになってから、公式として覚えていくよう




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち
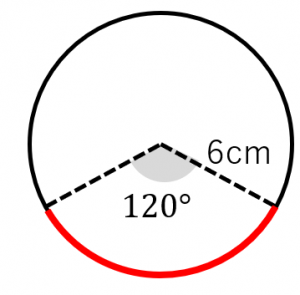
カンタン公式扇形の中心角の求め方がわかる3つのステップ 扇形の中心角の求め方の公式を知りたい! こんにちは、この記事をかいているKenだよー!豆乳ラテだったら3杯はいけるね。 「扇形の中心角の求め方」の公式 ってチョー便利。小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題 フォローをありがとうございます。 扇形は、円を分割してできた形なので、半径はどこも同じです。 なので、大きい扇形の半径は小さい扇形の半径と書いてある3センチを合わせて6センチとなります。 なので、大きい扇形の面積から、小さい扇形の面積を引いたものが、求めたい面積です。



面積の求め方 算数の教え上手 学びの場 Com




中1 数学 中1 75 おうぎ形の弧と面積 基本編 Youtube
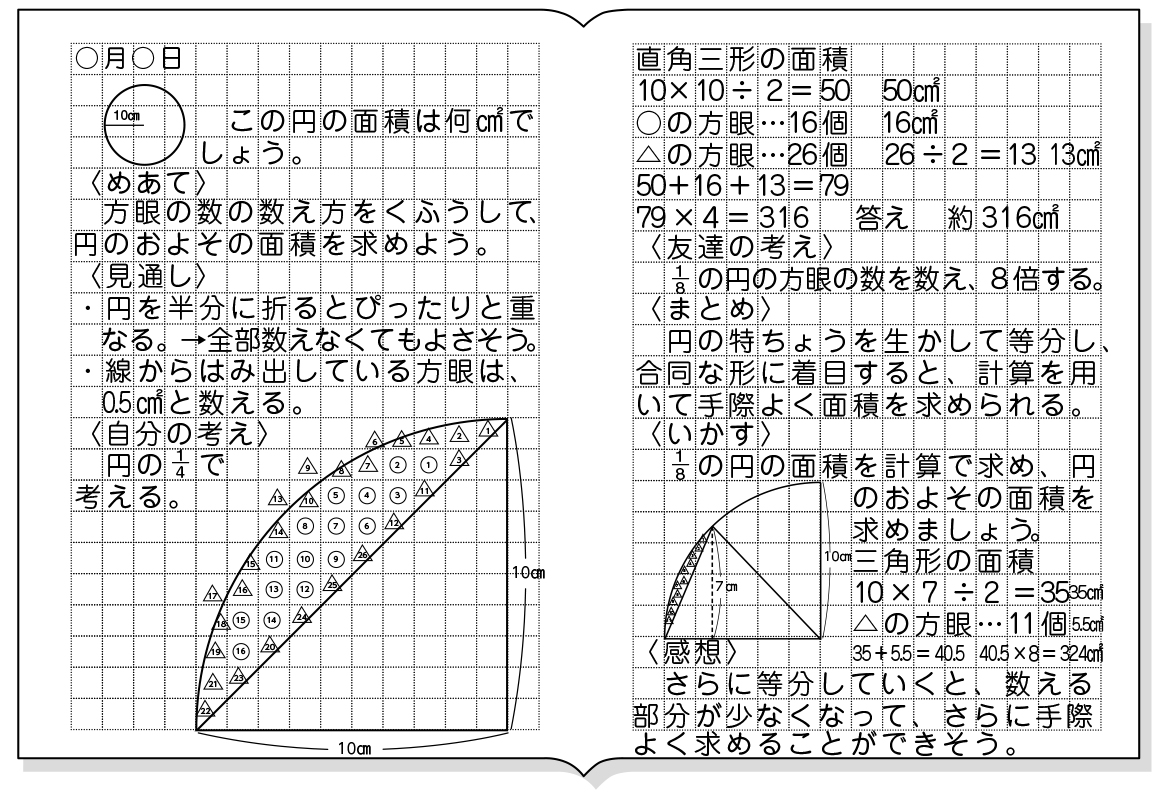
円周の求め方などを学習してきた。 本単元では、円の面積の求め方が主な学習 内容となる。第5学年までに基本的な平面図 形の意味や性質、図形の面積の意味、いろい ろな図形の面積の求め方の学習をしてきて いる。それを活かし、既習である図形に形を ここでは、おうぎ形と正方形が組み合わさった面積を求める問題を見ていきます。 おうぎ形と正方形の面積その1 例題1 次の図は、正方形とおうぎ形を組み合わせた図形です。色のついた部分の面積を求めなさい。 このような部分の面積 面積の求め方公式一覧 算数 面積・まわりの長さ 平面図形の面積・まわりの長さの求め方(公式)を一覧にまとめました。 公式を忘れてしまったときにはこちらで確認しましょう。 (基本的な問題もあわせて練習できるようになっています。 ) 円



弧の長さと弦の長さの求め方 円周角との関係など 具体例で学ぶ数学



おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun
a,b,c,d は合同なので a の面積だけの求め方を考える! a の部分の面積を求めるには左図の手順でよい! (扇形の面積)=π(10) 2 ÷6=(100/6)π 小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生 扇形 の 面積 の 求め 方 小学生2 θ b a ( b − a) cos 2 θ) r ( θ) 2 = a 2 b 2 b 2 cos 2 θ a 2 sin 2 θ ( 2) e l l i p t i c a l a r c h L = a E ( x ( θ 0) a, k) − a E ( x ( θ 1) a, k) x ( θ) = r ( θ) cos θ, k = 1 − ( b a) 2, a ≥ b, π 2 ≥ θ ≥ 0 E ( x, k) 2 n d i n c o m p l e t e e l l i p t i c i n t e g r a l



小6算数 円の面積 指導アイデア 1 みんなの教育技術




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく



正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく



面積 これが中学入試に出た図形問題




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




扇形の面積を半径 中心角 弧の長さから求める2通りの方法 偏差値40プログラマー




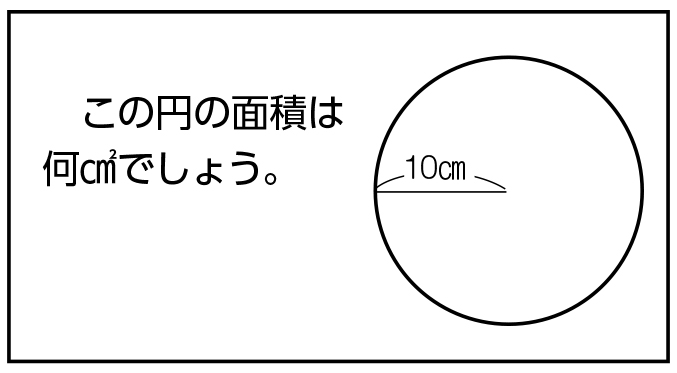
円の面積の求め方 公式と計算例




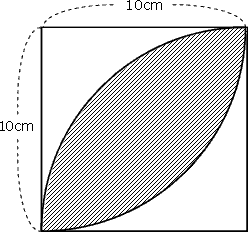
はっぱ型 の図形の面積 身勝手な主張



扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ
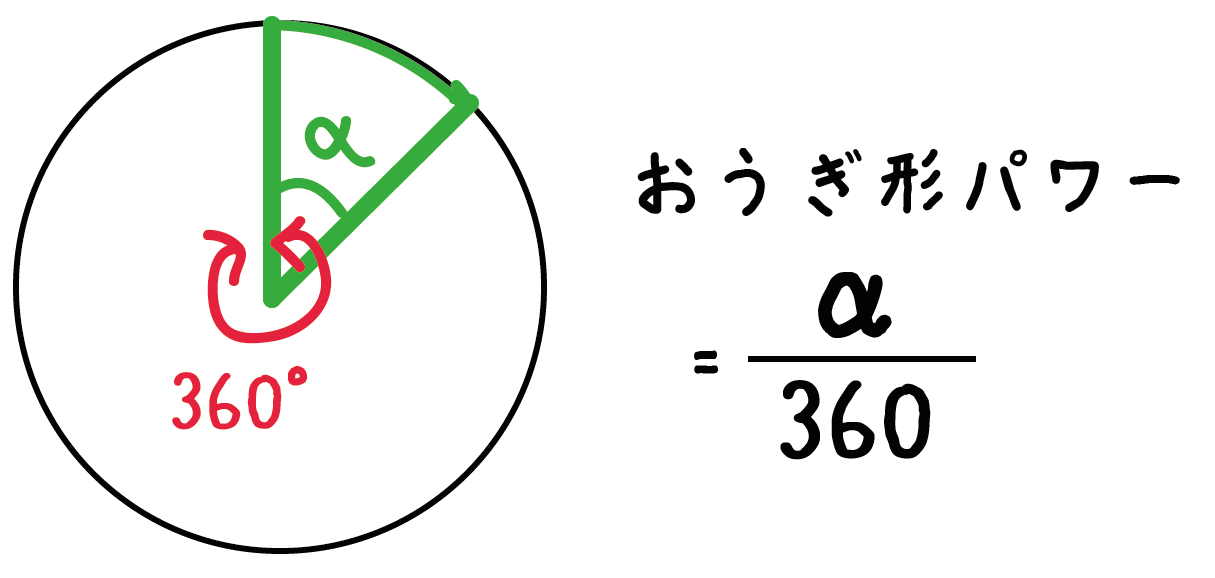



中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




円とおうぎ形 いろいろな面積の問題 中学受験準備のための学習ドリル



子供に説明できる 円の面積の公式 の証明 Nikkei Style




標準 おうぎ形と正方形の面積 なかけんの数学ノート




図形のまわりの長さが同じ場合 一番面積が大きい図形は 数学の面白いこと 役に立つことをまとめたサイト



小学算数の面積の求め方と公式一覧 四角形 長方形の性質や円の計算方法まで解説 学びtimes




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




公式を図解 すい体の体積 円すいの表面積の求め方



小学生の算数問題です扇形の面積を求めるのですが半径が10 角度は60 わか Yahoo 知恵袋




扇形 面積 公式 扇型の面積と中心角の求め方 扇型の問題は円の公式の理解がカギ Documents Openideo Com




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト




小5の算数 おうぎ形の面積は三角形の面積の公式で Youtube




半円を回転させる面積の問題 プリントを使って自分で解こう



弧 の 長 さ 公式 曲線の長さ Docstest Mcna Net




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく




この図形の色を塗った部分の面積の求め方を教えてください この図形 小学校 教えて Goo




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか




中学受験 高校受験 大学受験 興塾 正しい大人へ 先週 5 27 の解答 H28年度星陵中学入試問題




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生




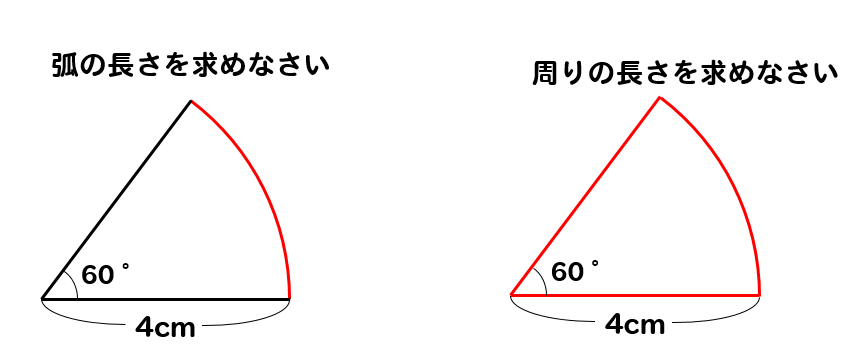
扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強




扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ




円の面積 円周の求め方 公式 小学生 中学生の勉強




扇形の面積 扇形の面積の求め方を教えてください 図は 大小2つの扇形 Okwave



Q Tbn And9gctj3goo5njmuwc 7pm2d T9knxkls8ofsc90dliywxdejwyqaiv Usqp Cau




小6 算数 小6 2 円の面積 応用編 Youtube
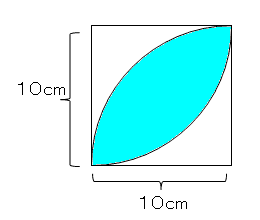



算数 扇形の面積の応用 葉っぱ型図形の面積 なるほどの素



対角線の求め方 小学生



おうぎ形 注意 周りの長さを求める公式を解説 数スタ



中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく



面積の求め方 算数の教え上手 学びの場 Com




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり




円とおうぎ形 応用 無料で使える中学学習プリント



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生




扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




扇形と扇形が重なっている部分の面積の解き方を教えてください 円周率 中学校受験 教えて Goo




円の面積はなぜ P R R なのか 公式の求め方を丁寧に解説 数学の面白いこと 役に立つことをまとめたサイト




扇形の面積の求め方 公式と計算例




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




数学の図形の面積についてです 画像の色のついた部分の面積の求め方 数学 教えて Goo




扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題



3




扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強




円の面積3 小学校6年生の教科書から つづき 身勝手な主張




小6 算数 小6 旧 円の面積 Youtube




面積の求め方 算数の教え上手 学びの場 Com



小6算数 円の面積 指導アイデア 1 みんなの教育技術




円の面積 円周の求め方 公式とやり方を解説 小学生向け 中学数学 理科の学習まとめサイト




円の周りの長さを計算しよう 家庭学習レシピ




おうぎ形 の弧の長さと面積 計算ドリル 問題集 数学fun




扇形の面積の求め方 公式と計算例



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題




円の面積の求め方 公式と計算例




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学




ボード 復習 のピン




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師




扇形 の 面積 の 求め 方 小学生 かわいいドラえもん




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく




中学1年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




色のついた部分の面積の求め方を教えてください Clear




円錐の表面積 中心角を求める問題を丁寧に解説 数スタ




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学




小学5年生の算数 円 おうぎ形 問題プリント ちびむすドリル 小学生




正方形の面積の求め方 小学生の子でもできるチョー簡単な問題 中学や高校の数学の計算問題




この問題の色をつけた部分の面積の求め方を教えて下さい 全く分から 中学校 教えて Goo
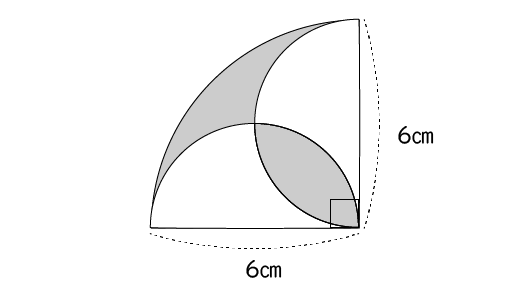



中学1年生数学 複雑な面積の求め方 長野地区 Itto個別指導学院 長野市の学習塾




円の面積 円周の求め方 公式 小学生 中学生の勉強



Q Tbn And9gcqfv9ekt Crg9bhcsz7q4t2e8znl6v2tplsqinzmz3lidwdpywk Usqp Cau




円の面積 練習応用 Youtube




Math 円錐の側面積が1秒で求められる公式 中学生 働きアリ



中学受験 図形の面積問題は 7つ道具 で攻略 かるび勉強部屋



小学生6年生です 扇形の面積を求めたいのですが 360分の1が 扇形の Yahoo 知恵袋




平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト



おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ



1




円の面積の公式 円周の求め方と間違えないようにしよう 中学や高校の数学の計算問題



0 件のコメント:
コメントを投稿